Gain Equalization (or Flattening) Filters

[ Contents ] [ Index ] [ Home ]

The terms "gain equalization" and "gain flattening" come from the fiberoptic telecommunications field, where erbium-doped fibers are used to amplify the light traveling through the fiber. These amplifiers have a wavelength-dependent gain; i.e., some wavelengths are amplified more than others. A gain-flattening filter restores all wavelengths to approximately the same intensity. Erbium-doped fiber amplifiers (EDFA) operate in the 1530-1565 nm wavelength range.

This type of filter has many applications. For example, for visible wavelengths 380-780 nm, a filter could be constructed to convert any continuous-spectrum illuminant into white light; e.g., light from an ordinary light bulb could be filtered to produce almost pure white light.

An introduction of the design of this filter can be found in the paper

    M. Tilsch, C.A. Hulse, K.D. Hendrix, R.B. Sargent, "Design and demonstration of a thin-film based gain equalization filter for C-band EDFAs", presented at the 1999 NFOEC conference.

The plot below shows the relative intensity of the EDFA output. If this were plotted on the logarithmic dB scale, the output would have a range of 8 dB.

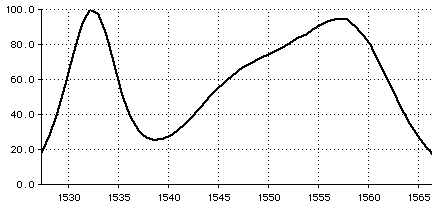
Plot of EDFA output

We will use TFCalc's optimization capabilities to design a gain-flattening reflection filter which will flatten (or equalize) the output of the EDFA so that it is flat with a tolerance of ±0.5 dB. In general, the tolerance is tighter for real filters.

TFCalc has the capability of optimizing the product of the illuminant (EDFA) and the reflectance (or transmittance) of a coating. We want this product, which is the actual output of the filter, to be a flat as possible. As can be seen from the plot shown above, even if the filter reflects (or transmits) a 100% at the endpoints (1527.3 and 1566.3 nm), the output would only be about 20%. Hence, for the entire wavelength range, the flattened output of the filtered EDFA can be no more than 20%. The design becomes somewhat easier if the target output is less than 20%.

Reflection Filter

Tilsch et al studied the reflection filter in their paper. To design such a filter, we started with the initial 100-layer design (HL)^50, where H represents 1.2 QWOT of index 2.25 and L represents 1.2 QWOT of index 1.45. The reference wavelength is 1530 nm. The substrate has index 1.44. We design this for normal incidence; in reality, the filter will be positioned at a small angle. For the optimization target we use

    EDFA * Reflectance = 17.5% for wavelengths from 1527.3 to 1566.3

A total of 201 equally-spaced targets are used. To make the output as flat as possible, we use power=16 during optimization. The result is a 91-layer design. In white light, the performance of the filter is shown below.

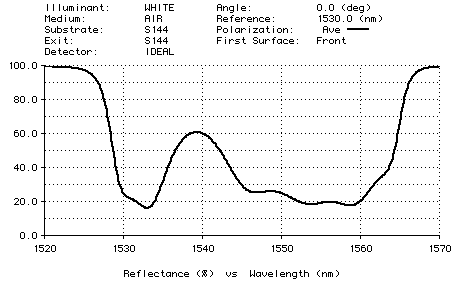
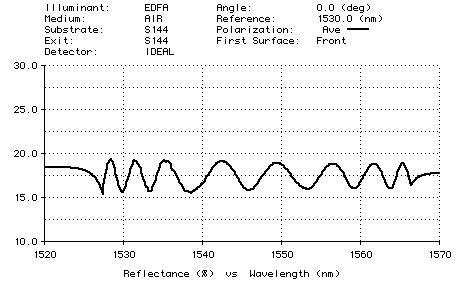
Plot of EDFA filter design

The plot below shows the output of the filtered EDFA. If this is plotted on a dB scale, it becomes apparent that the design, if it could be produced without errors, meets the ±0.5 dB requirement.

Plot of EDFA filter design

Transmission Filter

To discover whether there is any advantage in using a transmission filter, we decided to design one. Most of the details are the same as for the reflection filter. However, this time we started with the 101-layer design (HL)^50 H. The target is

    EDFA * Transmittance = 17.5% for wavelengths from 1527.3 to 1566.3

We used one continuous target. Again, we use power=16. By constraining the layer thicknesses to be greater than 0.5 QWOT during optimization, we discover a 101-layer design having a very flat (less than ±0.12 dB) output, as displayed below on a dB scale.

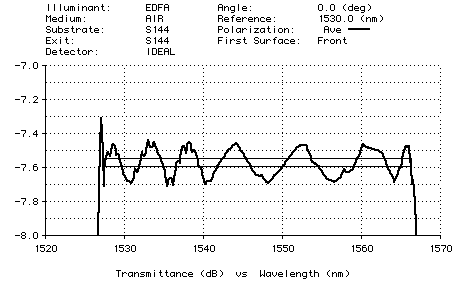
Plot of EDFA design

Manufacturability

By randomly varying the thickness of layers, TFCalc can determine the manufacturability of a design. For the designs mentioned in the Tilsch et al paper, a maximum error of 0.05% is required for production. Note that, using this error limit, if a layer is 100 nm thick, then the thickness must be monitored to within ±0.5 angstrom! The plot below shows the range of the performance of the reflection filter for 1000 random designs when layers are allowed to vary uniformly by ±0.05%.

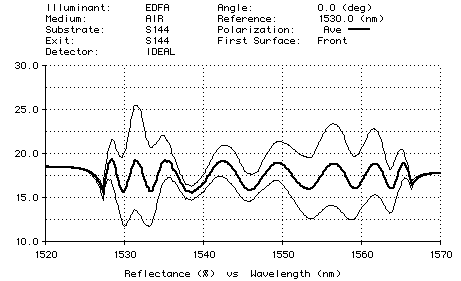
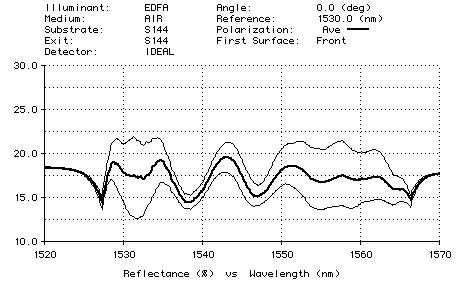
Plot of EDFA design

Even 0.05% seems barely acceptable. Using TFCalc's sensitivity optimization capability, we can try to find a design that is less sensitive to manufacturing errors. The procedure is rather slow, but the results may be worth the wait. We chose to optimize the sensitivity of 1000 random designs. On a 1 GHz Pentium, this requires several hours. Below is the sensitivity analysis of the improved design. Note that the optimizer has found a design that is significantly less sensitive to thickness errors.

Plot of EDFA design

Although the sensitivity optimization seems to work by making the performance of the filter flatter when the intensity of the EDFA is high, the optimizer actually does more. Numerical experiments show that, in general, merely designing a filter that is flatter where the EDFA intensity is high will still be very sensitive to thickness variations. The sensitivity optimization actual finds a less sensitive design, which also happens to have a flatter output at wavelengths where the EDFA has higher intensity.

This work is not nearly as exhaustive as in the Tilsch et al paper. However, it does show how optimizing the sensitivity can improve the performance of a design.

Here are the two designs; Design 1 is the original reflection design; Design 2 is the reflection design optimized for sensitivity. The first layer is closest to the substrate and thickness is given in nm: 

Material  Design1   Design2
N225      173.22    183.23
N145      266.11    283.45
N225      170.37    187.68
N145      281.70    310.91
N225      241.67    232.70
N145      499.80    486.55
N225      149.42    123.93
N145      216.86    239.55
N225      170.23    182.06
N145      276.29    300.51
N225      162.25    185.72
N145      260.42    264.95
N225      176.10    151.72
N145      249.71    215.61
N225      389.76    404.62
N145      244.24    250.29
N225      176.51    176.04
N145      269.84    258.26
N225      172.68    161.16
N145      351.00    358.60
N225      318.17    316.63
N145      285.93    279.08
N225      158.51    181.70
N145      246.70    282.89
N225      177.51    169.19
N145      290.04    253.96
N225      166.26    165.89
N145      265.69    263.71
N225      187.39    176.44
N145      311.12    322.47
N225      266.31    283.07
N145      353.44    322.81
N225      183.75    179.50
N145      268.79    273.76
N225      177.71    179.47
N145      267.34    275.20
N225      180.82    186.31
N145      265.61    285.18
N225      179.56    191.58
N145      310.69    307.51
N225      201.44    191.85
N145      337.80    335.97
N225      546.46    539.71
N145      419.51    418.70
N225      180.85    182.18
N145      261.04    270.87
N225      173.18    179.08
N145      264.37    276.37
N225      172.93    185.79
N145      264.15    256.11
N225      175.67    168.30
N145      265.07    260.12
N225      178.47    199.99
N145      251.01    244.43
N225      182.79    199.31
N145      596.29    582.84
N225      115.52    114.77
N145      244.92    217.38
N225      173.55    177.19
N145      263.13    271.27
N225      168.53    174.83
N145      265.62    276.17
N225      172.31    179.17
N145      264.86    274.15
N225      175.52    180.52
N145      280.45    288.85
N225      176.08    183.83
N145      243.23    239.70
N225      245.25    215.08
N145      177.49    231.26
N225      358.93    358.44
N145      262.76    255.62
N225      176.24    171.92
N145      245.65    223.47
N225      166.69    160.65
N145      255.30    259.85
N225      165.34    169.67
N145      256.16    275.05
N225      412.72    403.73
N145      239.67    218.93
N225      175.49    175.58
N145      273.85    297.29
N225      140.82    169.58
N145      297.28    309.52
N225      219.98    193.75
N145      493.44    484.74
N225      168.57    157.29
N145      282.43    319.13
N225      175.48    186.11
N145      274.12    303.92
N225      173.02    181.17
Copyright © 1995-2008 Software Spectra, Inc.